Er wordt vaak over gesproken. Het veelkleurige knopje op de toolbar is voor iedereen. Druk erop! Het is makkelijk! Gebruik het!
Is dat wel zo?
Handrekenen heb je geleerd op de lagere school. Staartdelingen en worteltrekken. Dat soort werk.
Gebruik je het nog wel eens? Ik denk zelden.
Schatten leer je als je buiten speelt. Haal ik die afstand over die sloot, met mijn schoenen, vanaf deze blubberige kant? Is dat touw sterk genoeg om aan te hangen en over de sloot heen te slingeren? Is deze wiebelige brug sterk genoeg om me te dragen?
Je doet heel veel ervaring op in je leven, maar je gebruikt het niet om te rekeken. Bijvoorbeeld: kan een m10 boutje mijn auto optillen?
Gebruik je het nog wel eens? Ik denk zelden.
Rekenlineaal 10^9 met logaritmische tabellen en goniometrische tabellen.

GFDL 1.2, https://commons.wikimedia.org/w/index.php?curid=647101
Gebruik je de lineaal en de tabellen nog wel eens? Ik denk zelden.
De zakrekenmachine was en is een fantastische uitvinding. Met een mooie nauwkeurigheid. Maar wat heb je er aan als je pi door twee moet delen en vervolgens het antwoord moet vermenigvuldigen met een geschat gewicht?

De uitkomsten worden nauwkeurig weergegeven, maar je moet zelf beoordelen hoeveel significante cijfers je gebruikt. Alle cijfers behalve voorafgaande nullen zijn significant: 87,636 heeft bijvoorbeeld vijf significante cijfers; 0,636 heeft er drie. Als een getal geen komma bevat, is het in het geval van een of meer nullen aan het eind, zoals 3620, 3600 en 3000, niet duidelijk of daar significante bij zijn, en zo ja hoeveel. Om aan te geven welke cijfers significant zijn, kan een getal als 3000 in de wetenschappelijke notatie worden genoteerd. Als drie cijfers significant zijn — de waarde ligt tussen 2995 en 3005 — noteert men 3,00 × 10³.
Gebruik je de rekenmachine nog wel eens? Ik denk het wel.
FEA (finite element analysis) methode. Is dit dan de juiste methode? Grote fouten worden gemaakt in de opzet van het model: singularities en te stijve constraints.
Wat is een singulariteit? Bekijk de wiskundige functie f(x)=1/x , waarbij x een positieve of negatieve waarde mag hebben. Dit werkt voor alle waardes van x (op de reële getallenlijn), tot het moment dat we 0 invullen. De vergelijking f(x)=1/0 levert een waarde op die niet gedefinieerd is. Grafisch weergegeven:
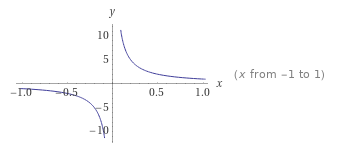
Oftewel een asymptoot. Dit geeft wel een probleempje, als je op zoek bent naar de hoogste spanning. Deze is namelijk oneindig.
Constraints of vastleggingen. Hoe ga je daar mee om? Een voorbeeld:
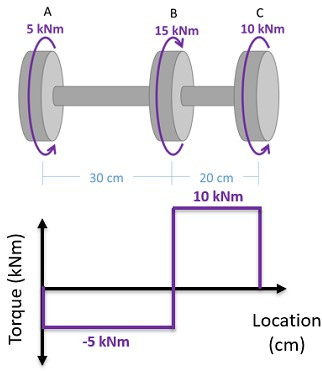
Eenvoudig toch? Even een asje modelleren als 1d element en klaar.
Maar wat als het een 3d solid model is? Hoe constrain je de lagering dan?
Dan ontkom je er niet aan om een deel van de support van de lagering te modelleren en met behulp van St Venant de vervormbaarheid van de lagers mee te nemen. En vergeet ook niet een van de lageringen vast te zetten en de rest vrij te laten in de axiale richting. Dat is de realiteit. Die moet je benaderen.
Gebruik je FEA nog wel eens? Ik denk het wel. Maar vergeet niet de andere methode’s. Gebruik schatten om een idee te krijgen van de afmeting van de constructie.
Gebruik je rekenmachine voor een globale som (en sla deze op in MathCad).
Gebruik FEA op de juiste manier en verkrijg een meer gedetaileerd antwoord.
Veel plezier!